��Ŀ����
����Ŀ����ͼ����֪��O��ֱ��AB�ϣ���һ��ֱ�����ǰ��ֱ�Ƕ�����ڵ�O����������OCD=60�㣬��OEF=45������OC��OE��ֱ��AB�ϣ�
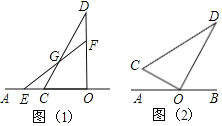
��1����ͼ��1������CD��EF�ཻ�ڵ�G������DGF�Ķ�����______�㣻
��2����ͼ��1���е����ǰ�OCD�Ƶ�O˳ʱ����ת30����ͼ��2��λ��
���������ǰ�OEF�Ƶ�O˳ʱ����ת180�����ڴ˹����У�����COE=��EOD=��DOFʱ������AOE�Ķ�����
���������ǰ�OEF�Ƶ�O��ÿ��4�����ٶ�˳ʱ����ת180�������ͬʱ�������ǰ�OCD�Ƶ�O��ÿ��1�����ٶ�˳ʱ����ת�������ǰ�OEF��ת���յ�λ��ʱ�����ǰ�OCDҲֹͣ��ת������תʱ��Ϊt�룬��OD��EFʱ����t��ֵ��
���𰸡���1��15����2��������COE=��EOD=��DOFʱ����AOE=75�㣻����OD��EFʱ��t��ֵΪ25��
��������
��1��������������ǵ����ʼ��ɵõ����ۣ�
��2������ͼ2��������֪���������COE=��EOD=45�����õ���AOE=��AOC+��COE=30��+45��=75��������COE=��EOD=��DOFʱ����ý��ۣ��ڸ��ݴ�ֱ�Ķ���õ�OD��EF���õ���OHE=90���з�����ý��ۣ�
��1���ߡ�EFO=45�㣬��D=30�㣬
���DGF=��EFO-��D=45��-30��=15�㣬
�ʴ�Ϊ��15��
��2������ͼ2��

�ߡ�COE=��EOD=��DOF����COE+��EOD=��COD����COD=90�㣬
���COE=��EOD=45�㣬
���AOE=��AOC+��COE=30��+45��=75�㣬
����COE=��EOD=��DOFʱ����AOE=75�㣻
�ڡߡ�AOE=4t�㣬��AOC=30��+t������ͼ3��
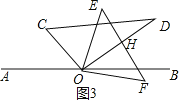
��OD��EF��
���OHE=90��
�ߡ�E=45�㣬��COD=90�㣬
���COE=45�㣬
���AOE-��AOC=��COE=45�㣬
��4t-��30+t��=45��
��t=25��
����OD��EFʱ��t��ֵΪ25��

����Ŀ����֪һ�κ���y��2x��2a��y����x��b��ͼ������A(��2��a)������x��ֱ���B��C���������ABC�����Ϊ________��
����Ŀ��ij����С���A�س������ڶ�������Ĺ�·�ϼ�����·������涨����ʻΪ����������ʻΪ����һ�����ߴ���ʻ����¼���£���λ��km��
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | ��6�� | ��7�� |
��4 | +7 | ��9 | +8 | +6 | ��5 | ��2 |
���չ�ʱ��A�ض�Զ���ڵڼ��μ�¼ʱ��A����Զ��
A. 2ǧ�� ��1�� B. 1ǧ�� ��2��
C. 2ǧ�� ��4�� D. 1ǧ�� ��5��