Question

【题目】在△ABC中，D为BC中点，BE、CF与射线AE分别相交于点E、F（射线AE不经过点D）.

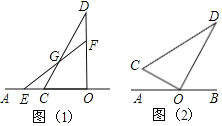
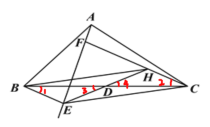
（1）如图①，当BE∥CF时，连接ED并延长交CF于点H. 求证：四边形BECH是平行四边形；

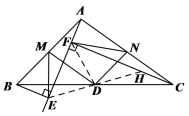
（2）如图②，当BE⊥AE于点E，CF⊥AE于点F时，分别取AB、AC的中点M、N，连接ME、MD、NF、ND. 求证：∠EMD=∠FND.

图① 图②

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据ASA证明△BDE≌△CDH.得ED=HD.又BD＝CD，可得四边形BECH是平行四边形.

（2）连接FD、ED，延长ED交CF于点H，根据（1）可知ED=HD.可得ED＝FD. 在Rt△AEB中，M是斜边AB中点，故 ,同理.故ME=DN 同理，MD=NF. 由SSS证△MED≌△NDF.所以∠EMD=∠FND.

证明：（1）∵D为BC中点，

∴BD＝CD.

∵BE∥CF，

∴∠1＝∠2.

又∵∠3＝∠4，

∴△BDE≌△CDH.

∴ED=HD.

∴四边形BECH是平行四边形.

（2）连接FD、ED，延长ED交CF于点H，

∵BE⊥AE，CF⊥AE，

∴BE∥CF.

根据（1）可知ED=HD.

又∵CF⊥AE，

∴ED＝FD.

∵Rt△AEB中，M是斜边AB中点，

∴ ,

∵△ABC中，D、N分别是BC、AC中点，

∴.

∴ME=DN

同理，MD=NF.

∴△MED≌△NDF.

∴∠EMD=∠FND.