题目内容
【题目】如图所示,在矩形ABCD中,E,F,G,H分别为边AB,BC,CD,DA的中点,若AB=2,AD=4,则图中阴影部分的面积为____.

【答案】4
【解析】
连接AC,BD,FH,EG,得出平行四边形ABFH,推出HF=AB=2,同理EG=AD=4,求出四边形EFGH是菱形,根据菱形的面积等于![]() ×GH×HF,代入求出即可.
×GH×HF,代入求出即可.
连接AC,BD,FH,EG,
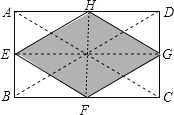
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴AH=![]() AD,BF=
AD,BF=![]() BC,
BC,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴AH=BF,AH∥BF,
∴四边形AHFB是平行四边形,
∴FH=AB=2,
同理EG=AD=4,
∵四边形ABCD是矩形,
∴AC=BD,
∵E,F,G,H分别为边AB,BC,CD,DA的中点,
∴HG∥AC,HG=![]() AC,EF∥AC,EF=
AC,EF∥AC,EF=![]() AC,EH=
AC,EH=![]() BD,
BD,
∴EH=HG,GH=EF,GH∥EF,
∴四边形EFGH是平行四边形,
∴平行四边形EFGH是菱形,
∴FH⊥EG,
∴阴影部分EFGH的面积是![]() ×HF×EG=
×HF×EG=![]() ×2×4=4,
×2×4=4,
故答案为:4.

练习册系列答案
相关题目




