题目内容
【题目】在平面直角坐标系中,点![]() ,
,![]() ,点C为x轴正半轴上一动点,过点A作
,点C为x轴正半轴上一动点,过点A作![]() 交y轴于点E.
交y轴于点E.

![]() 如图
如图![]() ,若点C的坐标为
,若点C的坐标为![]() ,试求点E的坐标;
,试求点E的坐标;
![]() 如图
如图![]() ,若点C在x轴正半轴上运动,且
,若点C在x轴正半轴上运动,且![]() , 其它条件不变,连接DO,求证:OD平分
, 其它条件不变,连接DO,求证:OD平分![]()
![]() 若点C在x轴正半轴上运动,当
若点C在x轴正半轴上运动,当![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)点E的坐标为(0,2);(2)详见解析;(3)∠OCB=60°.
【解析】
(1)先根据AAS判定△AOE≌△BOC,得出OE=OC,再根据点C的坐标为(2,0),得到OC=2=OE,进而得到点E的坐标;
(2)先过点O作OM⊥AD于点M,作ON⊥BC于点N,根据△AOE≌△BOC,得到S△AOE=S△BOC,且AE=BC,再根据OM⊥AE,ON⊥BC,得出OM=ON,进而得到OD平分∠ADC;
(3)在DA上截取DP=DC,连接OP,根据SAS判定△OPD≌△OCD,再根据三角形外角性质以及三角形内角和定理,求得∠PAO=30°,进而得到∠OCB=60°.
(1)如图①,∵AD⊥BC,BO⊥AO,
∴∠AOE=∠BDE,
又∵∠AEO=∠BED,
∴∠OAE=∠OBC,
∵A(-3,0),B(0,3),
∴OA=OB=3,
∴△AOE≌△BOC,
∴OE=OC,
又∵点C的坐标为(2,0),
∴OC=2=OE,
∴点E的坐标为(0,2);
(2)如图②,过点O作OM⊥AD于点M,作ON⊥BC于点N,
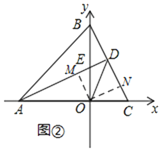
∵△AOE≌△BOC,
∴S△AOE=S△BOC,且AE=BC,
∵OM⊥AE,ON⊥BC,
∴OM=ON,
∴OD平分∠ADC;
(3)如所示,在DA上截取DP=DC,连接OP,
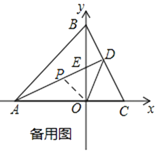
∵∠PDO=∠CDO,OD=OD,
∴△OPD≌△OCD,
∴OC=OP,∠OPD=∠OCD,
∵AD-CD=OC,
∴AD-DP=OP,即AP=OP,
∴∠PAO=∠POA,
∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB,
又∵∠PAO+∠OCD=90°,
∴3∠PAO=90°,
∴∠PAO=30°,
∴∠OCB=60°.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】已知:p为实数.
p | k | q |
… | … | … |
3 | 16×3+26 | 2×2×6 |
4 | 16×4+26 | 2×3×7 |
5 | 16×5+26 | 2×4×8 |
6 | 16×6+26 | 2×5×9 |
7 | 16×7+26 | 2×6×10 |
… | … | … |
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38?
(2)当p为何值时,k与q的值相等?