题目内容
【题目】如图(1),在![]() 和
和![]() 中,
中,![]() 为
为![]() 边
边![]() 上一点,
上一点,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.

(1)求证:![]()
(2)如图(2),若![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,
,![]() 为边
为边![]() 上一点,满足
上一点,满足![]() ,连接
,连接![]() 交
交![]() 于
于![]() . ①求
. ①求![]() 的度数;
的度数;
②若![]() 平分
平分![]() ,试说明:
,试说明:![]() 平分
平分![]() .
.
【答案】(1)见解析;(2)①60°;②见解析;
【解析】
(1)由角平分线定义得出∠ACB=∠ECD,由SAS证明△ABC≌△EDC即可;
(2)①由SAS证明△BCF≌△DCG,得出∠CBF=∠CDG,在△BCF和△DHF中,由三角形内角和定理得出∠DHF=∠ACB=60°即可;
②由全等三角形的性质得出∠DEC=∠A,由三角形的外角性质得出∠ECM=∠2+∠1=60°,∠DCM=∠A+∠ABC=120°,得出∠A+∠ABC=2(∠2+∠1)=2∠2+2∠1=2∠2+∠A,即可得出结论.
(1)证明:∵CA平分∠BCE,
∴∠ACB=∠ECD,
在△ABC和△EDC中,
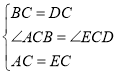
∴△ABC≌△EDC(SAS);
(2)①在△BCF和△DCG中, ,
,
∴△BCF≌△DCG(SAS);
∴∠CBF=∠CDG,
在△BCF和△DHF中,∵∠BFC=∠DFH,
∴∠DHF=∠ACB=60°;
②证明:如图(2)所示:

由(1)得:△ABC≌△EDC,
∴∠DEC=∠A,
∵∠ACB=∠ECD=60°,
∴∠ECM=60°,
∵EB平分∠DEC,
∴∠DEC=2∠1,
∵∠ECM=∠2+∠1=60°,∠DCM=∠A+∠ABC=120°,
∴∠A+∠ABC=2(∠2+∠1)=2∠2+2∠1=2∠2+∠A,
∴∠ABC=2∠2,
∴BE平分∠ABC.

【题目】已知:p为实数.
p | k | q |
… | … | … |
3 | 16×3+26 | 2×2×6 |
4 | 16×4+26 | 2×3×7 |
5 | 16×5+26 | 2×4×8 |
6 | 16×6+26 | 2×5×9 |
7 | 16×7+26 | 2×6×10 |
… | … | … |
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38?
(2)当p为何值时,k与q的值相等?





