题目内容
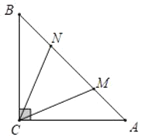
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=6![]() ,A,N是AB边上的两点,且满足∠MCN=45°,若AM=3,则MN的长为_____.
,A,N是AB边上的两点,且满足∠MCN=45°,若AM=3,则MN的长为_____.
【答案】5
【解析】
将△CBN顺时针旋转90度得到△ACR,连接RM得到△CRA≌△CNB全等BN=AR,再证△CNM≌△CRM,即可得到MR=MN,再证△ARM是直角三角形并利用勾股定理解三角形即可.
解:如图,将△CBN顺时针旋转90度,得到△ACR,连接RM
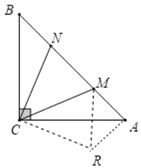
则△CRA≌△CNB全等,
∴AR=BN,∠B=∠CAR,∠BCN=∠ACR,
∵∠ACB=90°,AC=BC=6![]() ,
,
∴AB=12,∠B=∠CAB=45°,
∴∠CAR=45°,
∴∠MAR=90°,
∵∠MCN=45°,
∴∠BCN+∠ACM=45°=∠ACM+∠ACR,
∴∠MCN=∠MCR,且CN=CR,CM=CM,
∴△CNM≌△CRM(SAS)
∴MN=MR,
∵AB=12,AM=3,
∴BN+MN=9,
∴BN=AR=9﹣MN,
∵MR2=AM2+AR2,
∴MN2=(9﹣MN)2+9,
∴MN=5
故答案为5.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目