��Ŀ����
����Ŀ��ijѧУ�ƻ�����һƬ�յؽ�һ��ѧ�����г��������һ�濿ǽ�����ǽ�ij���Ϊ12�ף��ƻ����쳵������Ϊ80ƽ���ף���֪���е�ľ����Ͽ�ʹ�½���ǽ���ܳ�Ϊ26�ף�
(1)Ϊ�˷���ѧ�����У�ѧУ��������ǽƽ�е�һ�濪һ��2�����ţ���ô�������ij��Ϳ��ֱ�ӦΪ�����ף�
(2)��ͼ��Ϊ�˷���ѧ��ȡ����ʩ����λ�����ڳ������������ȿ���С·��ʹ��ͣ�����г������Ϊ54ƽ���ף���ôС·�Ŀ�Ϊ�����ף�
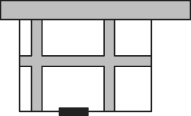
���𰸡���1����Ϊ10�ף���Ϊ8�ף���2��С·�Ŀ�Ϊ1�ף�
��������
��1������ǽ��ֱ��һ��Ϊx�ף�Ȼ��ɵ���������Ϊ��26-2x+2���ף�Ȼ�����������Ϊ80�г�������⼴�ɣ�
��2����С·�Ŀ�Ϊa�ף�����ȥ��С·�����Ϊ54ƽ���г�������⼴�ɵõ��𰸣�
�⣺��1������ǽ��ֱ��һ��Ϊx�ף���һ����Ϊ��26-2x+2����
��������ã�x��28-2x��=80
�����ã�x2-14x+40=0
���x=4��x=10��
��x=4ʱ��28-2x=20��12����ȥ��
��x=10ʱ��28-2x=8��12
�Ϊ10�ף���Ϊ8�ף�
��2�����Ϊa�ף���������ã���8-2a����10-a��=54��
a2-14a+13=0��
��ã�a=13��10����ȥ����a=1��
��С·�Ŀ�Ϊ1�ף�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ�����������1������2������3�����ǰ�һ���������е�һ�з��̣�
��� | ���� | ���̵Ľ� | |
1 | x2+x��2����0 | x1����2 | x2��1 |
2 | x2+2x��8����0 | x1����4 | x2��2 |
3 | x2+3x��18��0 | x1���� �� | x2���� �� |
�� | �� | �� | �� |
��1���ⷽ��3���������Ľ����ڱ��еĿհ״���
��2����д�����з����е�10�����̣����������ʽ����⣮
��3�����ݱ��еĹ���д����n�����̺�������̵Ľ⣮