题目内容
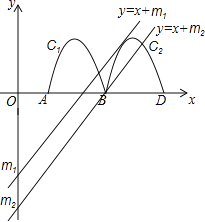
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )

A. ﹣2<m<![]() B. ﹣3<m<﹣
B. ﹣3<m<﹣![]() C. ﹣3<m<﹣2 D. ﹣3<m<﹣
C. ﹣3<m<﹣2 D. ﹣3<m<﹣![]()
【答案】D
【解析】令y=﹣2x2+8x﹣6=0,
即x4x+3=0,
解得x=1或3,
则点A(1,0),B(3,0),
由于将C向右平移2个长度单位得C,
则C解析式为y=2(x4) +2(3x5),
当y=x+m与C相切时,
令y=x+m=y=2(x4) +2,
即2x15x+30+m=0,
△=8m15=0,
解得m=![]() ,
,
当y=x+m过点B时,
即0=3+m,
m=3,
当3<m<![]() 时直线y=x+m与C、C共有3个不同的交点,
时直线y=x+m与C、C共有3个不同的交点,
故选:D.
点睛:本题主要考查抛物线与x轴交点以及二次函数图象与几何变换的知识,解答本题的关键是正确地画出图形,利用数形结合进行解题,此题由一定的难度.

【题目】根据下列表格回答问题:
x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(1)268.96的算术平方根是__________;
(2)![]() =___________;
=___________;
(3)![]() 在哪两个相邻的一位小数之间?为什么?
在哪两个相邻的一位小数之间?为什么?
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850

对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)求m,n的值;
(2)补全频数分布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组?
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.