题目内容
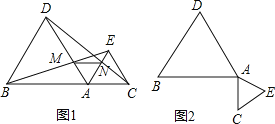
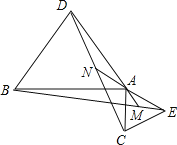
【题目】如图1,点A是线段BC上一点,△ABD,△AEC都是等边三角形,BE交AD于点M,CD交AE于N.
(1)求证:BE=DC;
(2)求证:△AMN是等边三角形;
(3)将△ACE绕点A按顺时针方向旋转90°,其它条件不变,在图2中补出符合要求的图形,并判断(1)、(2)两小题结论是否仍然成立,并加以证明.
【答案】(1)证明见详解;(2)证明见详解;(3)(1)的结论成立,(2)的结论不成立,证明见详解
【解析】
(1)根据等边三角形的性质得到AB=AD,AC=AE,∠DAB=∠EAC=60°,则∠DAC=∠BAE,根据“SAS"可判断△ABE≌△ADC,则BE= DC;
(2)由△ABE≌△ADC得到∠ABE=∠ADC,根据"AAS"可判断△ABM≌△ADN(AAS),则AM=AN;∠DAE=60°,根据等边三角形的判定方法可得到△AMN是等边三角形.
(3)判定结论1是否正确,也是通过证明△ABE≌△ADC求得,这两个三角形中AB=AD,AE=AC,∠BAE和∠CAD都是60°+∠ACB,因此两三角形就全等BE=CD,结论1正确;将△ACE绕点A按顺时针方向旋转90°,则∠DAC> 90°,因此三角形AMN绝对不可能是等边三角形.
解:(1)∵△ABD,△AEC都是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,
在△ABE和△ADC中,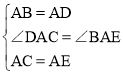 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC;
(2)由上述(1)证得:△ABE≌△ADC,
∴∠ABM=∠ADN.
在△ABM和△ADN中,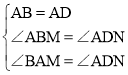 ,
,
∴△ABM≌△ADN(AAS),
∴AM=AN.
∵∠DAE=60°,
∴△AMN是等边三角形;
(3)∵△ABD,△AEC都是等边三角形,
∴AB=AD,AC=AE,∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,
在△ABE和△ADC中,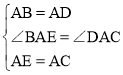 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC,∠ABE=∠ADC,
∵∠BAC=90°
∴∠MAN>90°,
∵∠MAN≠60°,
∴△AMN不是等边三角形,
∴(1)的结论成立,(2)的结论不成立.

 阅读快车系列答案
阅读快车系列答案【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:
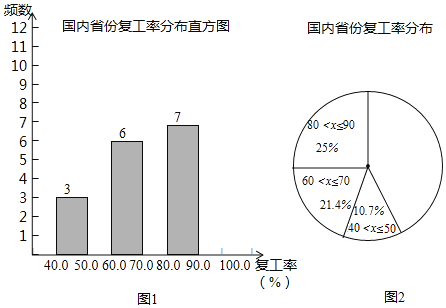
a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期 | 平均数 | 中位数 | 众数 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.