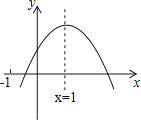题目内容
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.
(1)求证:DC是⊙O的切线;
(2)若OE=![]() cm,AC=
cm,AC=![]() cm,求DC的长(结果保留根号).
cm,求DC的长(结果保留根号).
【答案】
(1)
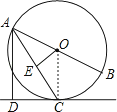
【解答】证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAD,
∴∠DAC=∠OAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∴∠ADC=∠OCF,
∵AD⊥DC,
∴∠ADC=90°,
∴∠OCF=90°,
∴OC⊥CD,
∵OC为半径,
∴CD是⊙O的切线.
(2)
∵OE⊥AC,
∴AE=![]() AC=
AC=![]() cm,
cm,
在Rt△AOE中,AO=![]() =4cm,
=4cm,
由1得∠OAC=∠CAD,∠ADC=∠AEO=90°,
∴△AOE∽△ACD,
∴![]() ,
,
即![]() ,
,
∴DC=![]() cm.
cm.
【解析】
【考点精析】掌握切线的判定定理和相似三角形的判定与性质是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】在刚刚闭幕的2016全国“两会”,民生话题依然是社会焦点,某市记者为了了解百姓对“两会民生话题”的聚焦点,随机调查了部分市民,并对调查结果进行整理.绘制了如图所示的统计图表(不完整). 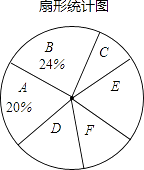
頻数分布表
组别 | 焦点话题 | 频数(人数) |
A | 医疗卫生 | 100 |
B | 食品安全 | m |
C | 教育住房 | 40 |
D | 社会保障 | 80 |
E | 生态环境 | n |
F | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= , n= . 扇形统计图中E组,F组所占的百分比分别为、
(2)该市现有人口大约800万,请你估计其中关注B组话题的人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注A组话题的概率是多少?
【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.