Question

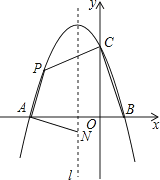
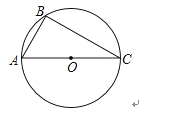
【题目】已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：①abc＞0，②a﹣b+c＜0，③2a=b，④4a+2b+c＞0，⑤若点（﹣2，y1）和（，y2）在该图象上，则y1＞y2 ． 其中正确的结论是 （填入正确结论的序号）．

Answer 1

【答案】②④
【解析】解：
∵二次函数开口向下，且与y轴的交点在x轴上方，
∴a＜0，c＞0，
∵对称轴为x=1，
∴﹣=1，
∴b=﹣2a＞0，
∴abc＜0，
故①、③都不正确；
∵当x=﹣1时，y＜0，
∴a﹣b+c＜0，
故②正确；
由抛物线的对称性可知抛物线与x轴的另一交点在2和3之间，
∴当x=2时，y＞0，
∴4a+2b+c＞0，
故④正确；
∵抛物线开口向下，对称轴为x=1，
∴当x＜1时，y随x的增大而增大，
∵﹣2＜﹣，
∴y1＜y2 ，
故⑤不正确；
综上可知正确的为②④，
所以答案是：②④．
【考点精析】根据题目的已知条件，利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案，需要掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．