题目内容
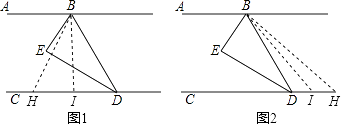
【题目】如图,已知,BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°. 
(1)求证:AB∥CD;
(2)H是直线CD上一动点(不与点D重合),BI平分∠HBD.写出∠EBI与∠BHD的数量关系,并说明理由.
【答案】
(1)证明:∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠EBD,∠BDC=2∠BDE,
∵∠EBD+∠EDB=90°,
∴∠ABD+∠BDC=2×90°=180°,
∴AB∥CD
(2)解:∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
如图1,点H在点D的左边时,∠ABH=∠ABD﹣∠HBD,
∠EBI=∠EBD﹣∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI,
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°﹣∠ABH,
∴∠BHD=180°﹣2∠EBI,
综上所述,∠BHD=2∠EBI或∠BHD=180°﹣2∠EBI.
【解析】(1)根据角平分线的定义可得∠ABD=2∠EBD,∠BDC=2∠BDE,然后求出∠ABD+∠BDC=180°,再根据同旁内角互补,两直线平行证明;(2)根据角平分线的定义可得∠ABD=2∠EBD,∠HBD=2∠IBD,然后分点H在点D的左边和右边两种情况,表示出∠ABH和∠EBI,从而得解.
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目