题目内容
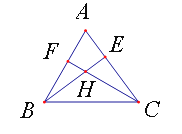
【题目】已知:如图,AE⊥BC,FG⊥BC,∠1=∠2 
(1)求证:AB∥CD
(2)若∠D=∠3+50°,∠CBD=80°,求∠C的度数.
【答案】
(1)证明:∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNM=90°,
∴AE∥FG,
∴∠A=∠2;
又∵∠2=∠1,
∴∠A=∠1,
∴AB∥CD
(2)解:∵AB∥CD,
∴∠D+∠CBD+∠3=180°,
∵∠D=∠3+50°,∠CBD=70°,
∴∠3=30°,
∵AB∥CD,
∴∠C=∠3=30°
【解析】(1)根据平行线的判定求出AE∥FG,根据平行线的性质得出∠A=∠2,求出∠A=∠1,根据平行线的判定得出即可;(2)根据平行线的性质得出∠D+∠CBD+∠3=180°,根据∠D=∠3+50°和∠CBD=70°求出∠3=30°,根据平行线的性质得出∠C=∠3即可.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】(本题10分)某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?