题目内容
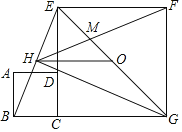
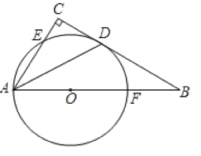
【题目】已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
A. 32![]() ﹣32﹣4πB.
﹣32﹣4πB. ![]() C. 1D. 16﹣4π
C. 1D. 16﹣4π
【答案】A
【解析】
连接OA、OB,作BI⊥OA于点I,作OM⊥AB于点M,求得△AOB的面积,则正八边形的面积即可求得,然后减去圆的面积即可求解.
解:连接OA、OB、JL、KM,作BI⊥OA于点I,作OM⊥AB于点M.
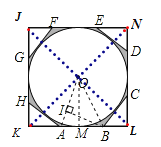
∵GF∥KN∥BC,AH∥JL∥DE,
∴△JGF, △KAH,CLB,END都是等腰直角三角形且全等,
∴∠HGF=∠GFE=∠FED=∠EDC=∠DCB=∠CBA=∠BAH=∠AHG=135°,
由切线长定理可知,GF=EF=DE=CD=BC=AB=AH=GH,
∴八边形ABCDEFGH是正八边形.
则∠AOB= ![]() =45°,
=45°,
∴△OBI是等腰直角三角形,
设AM=BM=x,则OA=OB=![]() ,OI=BI=
,OI=BI=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),
∴AB=![]() ,
,
则S△AOB=![]() ABOM=
ABOM=![]() ×(
×(![]() )×2=4
)×2=4![]() -4,
-4,
则正八边形ABCDEFGH的面积是8(4![]() -4)=32
-4)=32![]() -32.
-32.
⊙O的面积是:4π,
则阴影部分的面积为:32![]() -32-4π.
-32-4π.
故选:A.

练习册系列答案
相关题目