题目内容
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.

(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)连接OD,只需证明OD⊥DE.根据正方形的性质得到AE=AD,则∠ADE=45°.又∠ADO=45°则证明了结论;
(2)作OM⊥AB于M.根据平行线分线段成比例定理进行证明.
试题解析:证明:(1)连接OD.
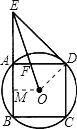
∵四边形ABCD为正方形,AE=AB.
∴AE=AB=AD,∠EAD=∠DAB=90°,
∴∠EDA=45°,∠ODA=45°,
∴∠ODE=∠ADE+∠ODA=90°,
∴直线ED是⊙O的切线.
(2)作OM⊥AB于M,
∵O为正方形的中心,
∴M为AB中点,
∴AE=AB=2AM,AF∥OM,
∴![]()
∴EF=2FO.
(2)作OM⊥AB于M.根据平行线分线段成比例定理进行证明.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目