题目内容
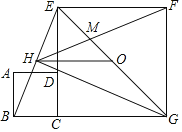
【题目】如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③![]() ﹣1;④
﹣1;④![]() =2﹣
=2﹣![]() ,其中正确的结论是( )
,其中正确的结论是( )
A. ①②③B. ①②④C. ①③④D. ②③④
【答案】A
【解析】
由四边形ABCD和四边形CGFE是正方形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得GH⊥BE;由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得HO∥BG且HO=![]() BG;由△EHG是直角三角形,因为O为EG的中点,所以OH=OG=OE,得出点H在正方形CGFE的外接圆上,根据圆周角定理得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,从而证得△EHM∽△GHF;设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,由HO∥BG,得出△DHN∽△DGC,即可得出
BG;由△EHG是直角三角形,因为O为EG的中点,所以OH=OG=OE,得出点H在正方形CGFE的外接圆上,根据圆周角定理得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,从而证得△EHM∽△GHF;设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,由HO∥BG,得出△DHN∽△DGC,即可得出![]() ,得到
,得到![]() ,即a2+2ab-b2=0,从而求得
,即a2+2ab-b2=0,从而求得![]() ,设正方形ECGF的边长是2b,则EG=2
,设正方形ECGF的边长是2b,则EG=2![]() b,得到HO=
b,得到HO=![]() b,通过证得△MHO△MFE,得到
b,通过证得△MHO△MFE,得到![]() ,进而得到
,进而得到![]() ,进一步得到
,进一步得到![]() .
.
解:如图,
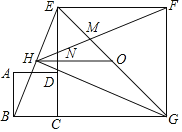
∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,
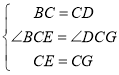
∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①正确;
∵△EHG是直角三角形,O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
∵EF=FG,
∴∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,
∴△EHM∽△GHF,
故②正确;
∵△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中点,
∴HO∥BG,
∴△DHN∽△DGC,
![]()
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
![]()
即a2+2ab﹣span>b2=0,
解得:a=b=(﹣1+![]() )b,或a=(﹣1﹣
)b,或a=(﹣1﹣![]() )b(舍去),
)b(舍去),
![]()
![]()
故③正确;
∵△BGH≌△EGH,
∴EG=BG,
∵HO是△EBG的中位线,
∴HO=![]() BG,
BG,
∴HO=![]() EG,
EG,
设正方形ECGF的边长是2b,
∴EG=2![]() b,
b,
∴HO=![]() b,
b,
∵OH∥BG,CG∥EF,
∴OH∥EF,
∴△MHO△MFE,
∴![]() ,
,
∴EM=![]() OM,
OM,
∴![]() ,
,
∴![]()
∵EO=GO,
∴S△HOE=S△HOG,
∴![]()
故④错误,
故选:A.

 字词句段篇系列答案
字词句段篇系列答案