题目内容
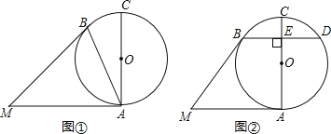
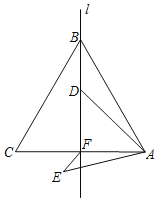
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
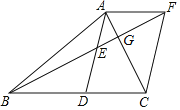
(1)求证:![]() ;
;
(2)若![]() ,①试判断四边形
,①试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
②若![]() ,
,![]() ,直接写出线段
,直接写出线段![]() 的长_________.
的长_________.
【答案】(1)见解析;(2)①四边形ADCF是菱形,证明见解析;②2
【解析】
(1)根据AF∥BC,得到∠AFE=∠DBE,再证全等即可;
(2)①先证四边形ADCF是平行四边形,再证AD=DC,从而证明ADCF是菱形;②证明△AFG∽△CBG,根据相似比求出![]() ,再根据勾股定理求出AC,从而求出AG长.
,再根据勾股定理求出AC,从而求出AG长.
证明:(1)∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD中点,
∴AE=DE,
在△AEF和△DEB中,

∴△AEF≌△DEB(AAS);
(2)①四边形ADCF是菱形,理由如下:
∵△AEF≌△DEB,
∴AF=BD,
∵BD=DC,
∴AF=DC=![]() BC,
BC,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,AD是BC边上的中线,
∴AD=DC,
∴四边形ADCF是菱形;
②∵AF∥BC
∴△AFG∽△CBG
∴![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴BC=2BD=10,
在Rt△ABC中,
![]() ,
,
∴AG=2.

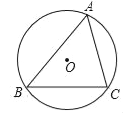
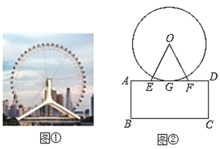
【题目】如图,AB 是⊙O 的弦,AB=5cm,点 P 是弦 AB 上的一个定点,点 C 是弧 AB 上的一 个动点,连接 CP 并延长,交⊙O 于点 D.
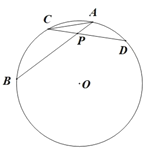
小明根据学习函数的经验,分别对 AC,PC,PD 长度之间的关系进行了探究.
下面是小明的探究过程:
(1)对于点 C 在弧 AB 上的不同位置,画图、测量,得到了线段 AC,PC,PD 的长度的 几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | 位置 9 | |
AC/cm | 0 | 0.37 | 1.00 | 1.82 | 2.10 | 3.00 | 3.50 | 3.91 | 5.00 |
PC/cm | 1.00 | 0.81 | 0.69 | 0.75 | 1.26 | 2.11 | 2.50 | 3.00 | 4.00 |
PD/cm | 4.00 | 5.00 | 5.80 | 6.00 | 3.00 | 1.90 | 1.50 | 1.32 | 1.00 |
在 AC,PC,PD 的长度这三个量中,确定___的长度是自变量,其他两条线段的长度都是这个自变量的函数;
(2)请你在同一平面直角坐标系 xOy 中, 画(1)中所确定的两个函数的图象;

(3)结合函数图象,解决问题:
①当 PC=PD 时,AC 的长度约为 cm;
②当△APC 为等腰三角形时,PC 的长度约为 cm.