题目内容
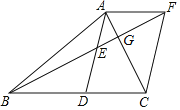
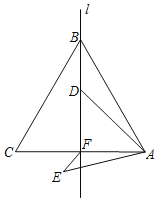
【题目】如图,等边三角形△ABC的边长为6,l是AC边上的高BF所在的直线,点D为直线l上的一动点,连接AD,并将AD绕点A逆时针旋转60°至AE,连接EF,则EF的最小值为_____.
【答案】![]()
【解析】
取AB的中点H,连接DH,由“SAS”可证△ADH≌△AEF,可得EF=DH,由垂线段最短,可得当DH⊥BF时,DH的长最短,即EF有最小值,即可求解.
解:如图,取AB的中点H,连接DH,
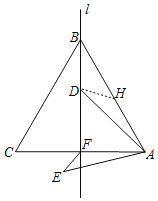
∵△ABC是等边三角形,BF是高,
∴AF=CF=3,∠ABF=30°,
∵点H是AB中点,
∴BH=AH=3,
∴AH=AF,
∵将AD绕点A逆时针旋转60°至AE,
∴AE=AD,∠DAE=60°=∠BAC,
∴∠DAH=∠FAE,且AF=AH,AD=AE,
∴△ADH≌△AEF(SAS)
∴EF=DH,
∴当DH⊥BF时,DH的长最短,即EF有最小值,
∴DH的最小值为![]() BH=
BH=![]() ,
,
∴EF的最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目