题目内容
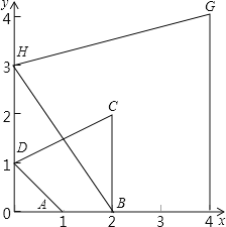
【题目】如图,点A.B在反比例函数y=![]() 的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
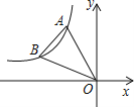
A.5B.-5C.4D.-4
【答案】B
【解析】
过A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,延长DB和CA交于点E,由点A.B的横坐标结合反比例函数图象上点的坐标特征即可求出A.B点的坐标,进而得出点E的坐标,再利用分割图形法求△AOB的面积结合S△AOB=3,即可得出关于k的一元一次方程,解方程即可得出结论.
过A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,延长DB和CA交于点E,如图所示.
∵点A、B在反比例函数y=![]() 的图象上,且点A,B的横坐标分别为a,2a(a<0),
的图象上,且点A,B的横坐标分别为a,2a(a<0),
∴A(a,![]() ),B(2a,
),B(2a,![]() ),E(2a,
),E(2a,![]() ),
),
∴OD=-2a,OC=![]() ,BE=
,BE=![]() ,AE=-a,其中k+1<0.
,AE=-a,其中k+1<0.
∴S△AOB=S矩形OCED-S△OBD-S△OAC-S△ABE=ODOC-![]() |k+1|-
|k+1|-![]() |k+1|-
|k+1|-![]() AEBE=3,
AEBE=3,
∵k+1<0,
∴-![]() (k+1)=3,
(k+1)=3,
解得:k=-5.
故选:B.

练习册系列答案
相关题目
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
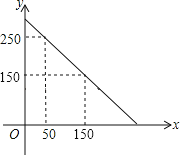
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.