题目内容
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
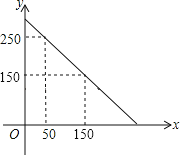
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.
【答案】(1) y=-x+300;(2) 至少购进多200甲种文具盒;(3)W=-3x+2400,最大利润1800元
【解析】
(1)利用待定系数法即可解决问题;
(2)构建不等式即可解决问题;
(3)根据一次函数,利用一次函数的性质即可解决问题;
(1)设y=kx+b,把(50,250),(150,150)代入得:
![]() ,
,
解得![]() ,
,
∴y=-x+300.
故答案是:y=-x+300.
(2)由题意:15x+30(-x+300)≤6000,
解得x≥200,
∴至少购进多200甲种文具盒.
(3)w=5x+8(-x+300)=-3x+2400,
∵y随x的增大而减少,x≥200,
∴x=200时,y有最大值,最大值=1800(元).

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目