题目内容
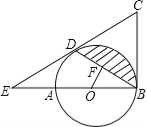
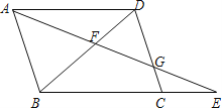
【题目】如图,E为ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.
(1)写出所有与△ABE相似的三角形,并选择其中一对相似三角形加以证明;
(2)若BC=2CE,求![]() 的值.
的值.
【答案】(1)①△ABE∽△GCE,②△ABE∽△GDA(2)![]()
【解析】
(1)根据“平行四边形的对边相互平行”可以推知AB∥DC,所以由平行线的性质得到,∠ABE=∠GCE,∠BAE=∠CGE,则△ABE∽△GCE;根据“平行四边形的对角相等.对边相互平行”可以推知:∠ABE=∠GDA,AD∥BE,根据平行线的性质得到∠E=∠DAG,则易证△ABE∽△GDA;
(2)易证得△ADF∽△EBF,根据相似三角形的对应边成比例可得![]() ,又由BC=2CE,即可求得
,又由BC=2CE,即可求得![]() 的值.
的值.
(1)①△ABE∽△GCE,②△ABE∽△GDA.
①证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠ABE=∠GCE,∠BAE=∠CGE,
∴△ABE∽△GCE.
②证明:∵四边形ABCD是平行四边形,
∴∠ABE=∠GDA,AD∥BE,
∴∠E=∠DAG,
∴△ABE∽△GDA.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△ADF∽△EBF,
∴![]() =
=![]() ,
,
∵BC=2CE,
∴AD:BE=2:3,
∴![]() =
=![]() .
.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
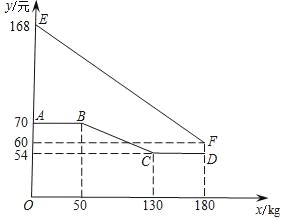
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
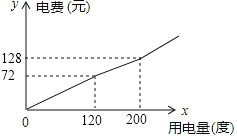
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?