ΧβΡΩΡΎ»ί
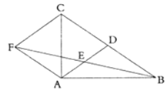
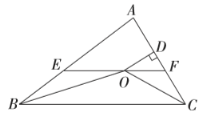
ΓΨΧβΡΩΓΩΡ≥≥ΒΩβ≥ωΩΎ¥Π…η÷Ο”–ΓΑΝΫΕΈ ΫάΗΗΥΓ±Θ§ΒψA «άΗΗΥΉΣΕ·ΒΡ÷ßΒψΘ§ΒψE «άΗΗΥΝΫΕΈΒΡΝ§Ϋ”ΒψΘ§Β±≥ΒΝΨΨ≠Ιΐ ±Θ§άΗΗΥAEF…ΐΤπΚσΒΡΈΜ÷Ο»γΆΦ1Υυ ΨΘ®ΆΦ2ΈΣΤδΦΗΚΈΆΦ–ΈΘ©Θ°Τδ÷–ABΓΆBCΘ§DCΓΆBCΘ§EFΓΈBCΘ§ΓœEAB=150ΓψΘ§AB=AE=1.2mΘ§BC=2.4mΘ°
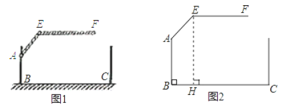
Θ®1Θ©«σΆΦ2÷–ΒψEΒΫΒΊΟφΒΡΗΏΕ»Θ®Φ¥EHΒΡ≥ΛΘ°![]() Γ÷1.73Θ§ΫαΙϊΨΪ»ΖΒΫ0.01mΘ§άΗΗΥΩμΕ»Κω¬‘≤ΜΦΤΘ©ΘΜ
Γ÷1.73Θ§ΫαΙϊΨΪ»ΖΒΫ0.01mΘ§άΗΗΥΩμΕ»Κω¬‘≤ΜΦΤΘ©ΘΜ
Θ®2Θ©»τ“ΜΝΨœα ΫΜθ≥ΒΒΡΩμΕ»ΚΆΗΏΕ»ΨυΈΣ2mΘ§’βΝΨ≥ΒΡήΖώ Μ»κΗΟ≥ΒΩβΘΩ«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©2.24ΟΉΘΜΘ®2Θ©’βΝΨ≥Β≤ΜΡή Μ»κΗΟ≥ΒΩβΘ§άμ”…¬‘.
ΓΨΫβΈωΓΩ
‘Χβ±ΨΧβΩΦ≤ιΝΥΫβ÷±Ϋ«»ΐΫ«–Έ‘Ύ ΒΦ ÷–ΒΡ”Π”ΟΘ§Ρ―Ε» ÷–Θ°ΙΊΦϋ «Ά®ΙΐΉςΗ®÷ζœΏΘ§ΙΙ‘λ÷±Ϋ«»ΐΫ«–ΈΘ§Α― ΒΦ Έ ΧβΉΣΜ·ΈΣ ΐ―ßΈ ΧβΦ”“‘ΦΤΥψ.Θ®1Θ©ΙΐΒψAΉςBCΒΡΤΫ––œΏANΘ§ΙΐΒψEΉςEHΓΆAG”ΎMΘ§‘ρΓœBAN=90ΓψΘ§ΓœEMA=90ΓψΘ°œ»«σ≥ωΓœEAM=60ΓψΘ§‘ρΓœEAM=60ΓψΘ§»ΜΚσ‘ΎΓςEAM÷–Θ§άϊ”Ο”ύœ“Κ· ΐΒΡΕ®“εΒΟ≥ωEM=AEcosΓœAEMΓ÷1.04ΟΉΘ§‘ράΗΗΥEFΕΈΨύάκΒΊΟφΒΡΗΏΕ»ΈΣΘΚAB+EMΘ§¥ζ»κ ΐ÷ΒΦΤΥψΦ¥Ω….Θ®2Θ©‘ΎAE…œ»Γ“ΜΒψPΘ§ΙΐΒψPΖ÷±πΉςBCΘ§CDΒΡ¥ΙœΏΘ§¥ΙΉψΖ÷±π «QΘ§RΘ§PRΫΜEH”ΎΒψKΘ§…ηPQΘΫ2ΟΉΘ§»ΜΚσΦΤΥψPR «Ζώ–Γ”Ύ2ΟΉΘ§‘ΌΫχ––≈–ΕœΦ¥Ω….
‘ΧβΫβΈωΘΚΫβΘΚΘ®1Θ©»γΆΦΘ§ΉςAMΓΆEH”ΎΒψMΘ§ΫΜCD”ΎΒψNΘ§
‘ρΥΡ±Ώ–ΈABHMΚΆMHCNΕΦ «ΨΊ–ΈΘ§
ΓΏΓœEABΘΫ150ΓψΘ§ΓύΓœEAMΘΫ60ΓψΘ§ Θ®1Ζ÷Θ©
”÷ΓΏABΘΫAEΘΫ1.2ΟΉΘ§
ΓύEMΘΫ![]() ΟΉΘ§Θ®3Ζ÷Θ©
ΟΉΘ§Θ®3Ζ÷Θ©
ΓύEHΓ÷2.24ΟΉ.
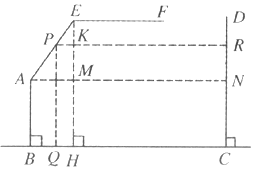
Θ®2Θ©»γΆΦΘ§‘ΎAE…œ»Γ“ΜΒψPΘ§ΙΐΒψPΖ÷±πΉςBCΘ§CDΒΡ¥ΙœΏΘ§
¥ΙΉψΖ÷±π «QΘ§RΘ§PRΫΜEH”ΎΒψKΘ§≤ΜΖΝ…ηPQΘΫ2ΟΉΘ§
œ¬ΟφΦΤΥψPR «Ζώ–Γ”Ύ2ΟΉΘΜ
”……œ ωΧθΦΰΩ…ΒΟEKΘΫEHΘ≠PQΘΫ0.24ΟΉΘ§AMΘΫ0.6ΟΉΘ§Θ®5Ζ÷Θ©
ΓΏPKΓΈAMΘ§ΓύΓςEPKΓΉΓςEAM. Θ®6Ζ÷Θ©
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ®7Ζ÷Θ©
Θ®7Ζ÷Θ©
Γύ![]() ΟΉ.Θ®8Ζ÷Θ©
ΟΉ.Θ®8Ζ÷Θ©
ΓύPRΘΫPKΘΪMNΘΫPKΘΪBCΘ≠AMΘΫ![]() .
.
![]() ΟΉΘ§ Θ®9Ζ÷Θ©
ΟΉΘ§ Θ®9Ζ÷Θ©
ΓΏPRΘΦ2ΟΉΘ§Γύ’βΝΨ≥Β≤ΜΡή Μ»κΗΟ≥ΒΩβ. Θ®10Ζ÷Θ©

 AΦ”ΫπΧβ œΒΝ–¥πΑΗ
AΦ”ΫπΧβ œΒΝ–¥πΑΗ »Ϊ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
»Ϊ”≈≤β ‘ΨμœΒΝ–¥πΑΗ