题目内容
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交C于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
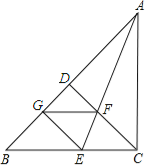
【答案】四边形GECF是菱形,理由详见解析.
【解析】
试题根据全等三角形的判定定理HL进行证明Rt△AEG≌Rt△AEC(HL),得到GE=EC;根据平行线EG∥CD的性质、∠BAC平分线的性质以及等量代换推知∠FEC=∠CFE,易证CF=CE;从而根据邻边相等的平行四边形是菱形进行判断.
试题解析:四边形GECF是菱形,理由如下:
∵∠ACB=90°,
∴AC⊥EC.
又∵EG⊥AB,AE是∠BAC的平分线,
∴GE=CE.
在Rt△AEG与Rt△AEC中,
![]() ,
,
∴Rt△AEG≌Rt△AEC(HL),
∴GE=EC,
∵CD是AB边上的高,
∴CD⊥AB,
又∵EG⊥AB,
∴EG∥CD,
∴∠CFE=∠GEA,
∵Rt△AEG≌Rt△AEC,
∴∠GEA=∠CEA,
∴∠CEA=∠CFE,即∠CEF=∠CFE,
∴CE=CF,
∴GE=EC=FC,
又∵EG∥CD,即GE∥FC,
∴四边形GECF是菱形.


练习册系列答案
相关题目