题目内容
【题目】已知在平面直角坐标系xOy中,直线l别交x轴和y轴于点A(-3,0),B(0,3).
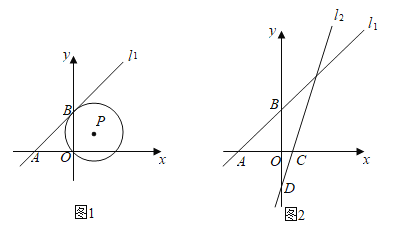
(1)如图1,已知⊙P经过点O,且与直线l1相切于点B,求⊙P的直径长;
(2)如图2,已知直线l2:y=3x-别交x轴和y轴于点C和点D,点Q是直线l2上的一个动点,以Q为圆心,2![]() 为半径画圆.
为半径画圆.
①当点Q与点C重合时,求证:直线l1与⊙Q相切;
②设⊙Q与直线l1相交于M,N两点,连结QM,QN.问:是否存在这样的点Q,使得△QMN是等腰直角三角形,若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①见解析;②(
;(2)①见解析;②(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)证明△ABC为等腰直角三角形,则⊙P的直径长=BC=AB,即可求解;
(2)证明![]() 圆的半径,即可求解;
圆的半径,即可求解;
(3)分点M、N在两条直线交点的下方、点M、N在两条直线交点的上方两种情况,分别求解即可.
解:(1)如图1,连接BC,
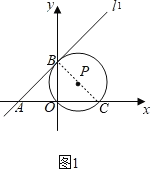
∵∠BOC=90°,∴点P在BC上,
∵⊙P与直线l1相切于点B,
∴∠ABC=90°,而OA=OB,
∴△ABC为等腰直角三角形,
则⊙P的直径长=BC=AB=![]() ;
;
(2)①过点作CM⊥AB,
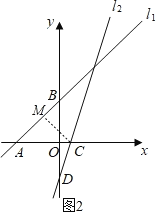
由直线l2:y=3x-3得:点C(1,0),
则![]() 圆的半径,
圆的半径,
故点M是圆与直线l1的切点,
即:直线l1与⊙Q相切;
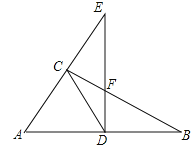
②如图3,
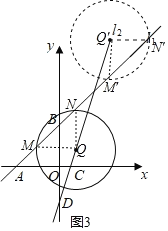
当点M、N在两条直线交点的下方时,
由题意得:MQ=NQ,∠MQN=90°,
设点Q的坐标为(m,3m-3),则点N(m,m+3),
则![]() ,
,
解得:![]() ;
;
当点M、N在两条直线交点的上方时,
同理可得:![]() ;
;
故点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目