题目内容
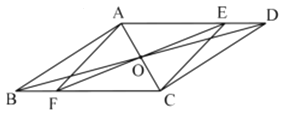
【题目】已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=BC=5,AB=6,求四边形AMCM的面积.

【答案】(1)见解析;(2)12.
【解析】
(1)由题意可得AB∥CD,AB=CD,又由M,N分别是AB和CD的中点可得AM=∥CN,即可得结论;
(2)根据等腰三角形的性质可得CM⊥AB,AM=3,根据勾股定理可得CM=4,则可求面积.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵M,N分别为AB和CD的中点,
∴AM=![]() AB,CN=
AB,CN=![]() CD,
CD,
∴AM=CN,且AB∥CD,
∴四边形AMCN是平行四边形;
(2)∵AC=BC=5,AB=6,M是AB中点,
∴AM=MB=3,CM⊥AM,
∴CM=![]() ,
,
∵四边形AMCN是平行四边形,且CM⊥SM,
∴AMCN是矩形,
∴S四边形AMCN=12.

练习册系列答案
相关题目
【题目】根据下表,回答问题:
x | … | -2 | -1 | 0 | 1 | 2 | … |
-2x+5 | … | 9 | 7 | 5 | 3 | a | … |
2x+8 | … | 4 | 6 | 8 | 10 | b | … |
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.