题目内容
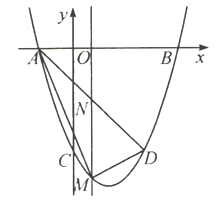
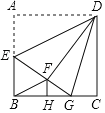
【题目】如图,正方形ABCD中,AB=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G,FH⊥BC,垂足为H,连接BF、DG.以下结论:①BF∥ED;②△DFG≌△DCG;③△FHB∽△EAD;④tan∠GEB=![]() ;⑤S△BFG=2.6;其中正确的个数是( )
;⑤S△BFG=2.6;其中正确的个数是( )
A.2B.3C.4D.5
【答案】C
【解析】
利用正方形的性质和折叠的性质可得∠AED=∠FED,AD=FD,AE=EF,∠A=∠DFE,即可判定①;证明Rt△DFG≌Rt△DCG,即可判定②;证明△FHB∽△EAD,即可判定③;设FG=CG=x,则BG=6﹣x,EG=3+x,再利用勾股定理即可判定④;设FH=a,则HG=4﹣2a,再利用勾股定理即可判定⑤
∵正方形ABCD中,AB=6,E为AB的中点
∴AD=DC=BC=AB=6,AE=BE=3,∠A=∠C=∠ABC=90°
∵△ADE沿DE翻折得到△FDE
∴∠AED=∠FED,AD=FD=6,AE=EF=3,∠A=∠DFE=90°
∴BE=EF=3,∠DFG=∠C=90°
∴∠EBF=∠EFB
∵∠AED+∠FED=∠EBF+∠EFB
∴∠DEF=∠EFB
∴BF∥ED
故结论①正确;
∵AD=DF=DC=6,∠DFG=∠C=90°,DG=DG
∴Rt△DFG≌Rt△DCG
∴结论②正确;
∵FH⊥BC,∠ABC=90°
∴AB∥FH,∠FHB=∠A=90°
∵∠EBF=∠BFH=∠AED
∴△FHB∽△EAD
∴结论③正确;
∵Rt△DFG≌Rt△DCG
∴FG=CG
设FG=CG=x,则BG=6﹣x,EG=3+x
在Rt△BEG中,由勾股定理得:32+(6﹣x)2=(3+x)2
解得:x=2
∴BG=4
∴tan∠GEB=![]()
故结论④正确;
∵△FHB∽△EAD,且![]()
∴BH=2FH
设FH=a,则HG=4﹣2a
在Rt△FHG中,由勾股定理得:a2+(4﹣2a)2=22
解得:a=2(舍去)或a=![]()
∴S△BFG=![]() ×4×
×4×![]() =2.4
=2.4
故结论⑤错误;
故选:C.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案