Question

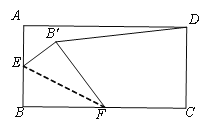
【题目】如图，CD是直角△ABC斜边上的中线，过点D作垂直于AB的直线交BC于点F，交AC的延长线于点E.

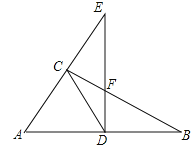
（1）求证：△ADE∽△FDB；

（2）若DF＝2，EF＝6，求CD的长．

Answer 1

【答案】（1）见解析；（2）4

【解析】

（1）根据题意，得∠A+∠B=90°，∠A+∠E=90°，则∠E=∠B，易证△ADE∽△FDB；
（2）由Rt△ABC中，CD是斜边上的中线，得AD＝CD＝BD＝AB，由（1）中的结论，得出＝，进一步整理代入求得答案即可．

（1）证明：∵DE⊥AB，

∴∠ADE＝∠FDB＝90°，

∴∠A＋∠E＝90°，

∵Rt△ABC中∠A＋∠B＝90°，

∴∠E＝∠B，

∴△ADE∽△FDB

（2）解：∵CD是直角△ABC斜边上的中线，

∴AD＝CD＝BD＝AB，

∵△ADE∽△FDB，

∴＝，

∵DF＝2，EF＝6，

∴DE＝8

∴＝，

∴AB=8，

∴CD＝4．