��Ŀ����
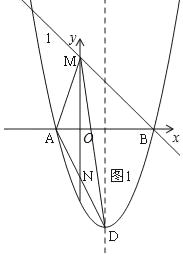
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��ax2����a+1��x��3��x�ύ��A��B���㣬��A������Ϊ����1��0����
��1����B���붥��D�����ꣻ
��2��������B��ֱ��l��y�������ύ�ڵ�M��S��ADM��5����ֱ��l�Ľ���ʽ��
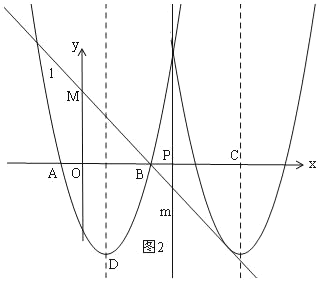
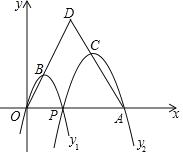
��3����P��t��0��Ϊx����һ���㣬����P��x��Ĵ���m������������ֱ��m���IJ�����ֱ��m���ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ����ͼ��G������ͼ��ش𣺵�ͼ��G��ֱ��lû�й�����ʱ��t��ȡֵ��Χ���� ����
���𰸡���1��D��1����4����B��3��0������2��y����x+3����3��![]() ��
��
��������
��1���ѵ�A�����꣨-1��0������y=ax2-��a+1��x-3�У������a��ֵ���䷽��ɵö���D�����꣬�ɶԳ��Կɵõ�B�����ꣻ
��2�����������ε����=Ǧֱ�߶���ˮƽ���ȵĻ����е�ʽ���ɵ�OM�ij���д��M�����꣬���ô���ϵ������ֱ��l�Ľ���ʽ��
��3�����ݶ��۵����ʵ��������ߵĶ������꣬�ɿ�����ͬ��֪��a=1���ɵý���ʽ����ͼ��G��ֱ��lû�й�����ʱ����������ʽ�����������⣬�ɵý��ۣ�
�⣺��1���ѵ�A�����꣨��1��0������y��ax2����a+1��x��3�У�
�ã�a+��a+1����3��0��
a��1��
��y��x2��2x��3����x��1��2��4��
��D��1����4����
�ɶԳ��Եã�B��3��0����
��2����ֱ��AD�Ľ���ʽΪ��y��kx+b��
��![]() ��
��
��ã�![]() ��
��
��ֱ��AD�Ľ���ʽΪ��y����2x��2��
��AD��y����N��
��ON��2��
��S��ADM��![]() MN����xA+xD����5��
MN����xA+xD����5��
��![]() ��2+OM������1+1����5��
��2+OM������1+1����5��
OM��3��
��M��0��3����
��ֱ��l�Ľ���ʽΪ��y��kx+b��
��![]() ��
��
��ã�![]() ��
��
ֱ��l�Ľ���ʽΪ��y����x+3��
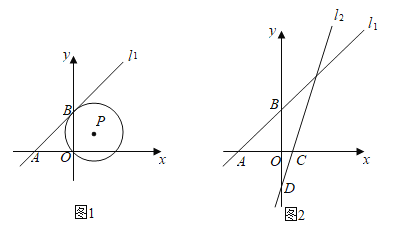
��3����ͼ2���ɶ��۵ã�OC��3+2��t��3��+2��2t��1��
���������ߵĶ���Ϊ��2t��1����4����
����ʽΪ��y����x��2t+1��2��4��
��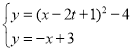 ��
��
��x��2t+1��2��4����x+3��
x2����4t��3��x+4t2��4t��6��0��
������0ʱ��ͼ��G��ֱ��lû�й����㣬
������[����4t��3��]2��4��4t2��4t��6����0��
t��![]() ��
��
�ʴ�Ϊ����