Question

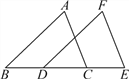
【题目】如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC中点，DE⊥AB，垂足为E，交AC的延长线于点F．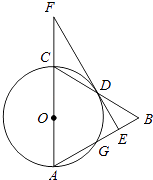
（1）求证：直线EF是⊙O的切线；
（2）若CF=5，cosA= ，求BE的长．

Answer 1

【答案】
（1）证明：如图，连结OD．

∵CD=DB，CO=OA，

∴OD是△ABC的中位线，

∴OD∥AB，AB=2OD，

∵DE⊥AB，

∴DE⊥OD，即OD⊥EF，

∴直线EF是⊙O的切线

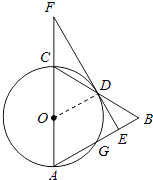
（2）解：∵OD∥AB，

∴∠COD=∠A．

在Rt△DOF中，∵∠ODF=90°，

∴cos∠FOD= = ，

设⊙O的半径为R，则 = ，

解得R= ，

∴AB=2OD= ．

在Rt△AEF中，∵∠AEF=90°，

∴cosA= = = ，

∴AE= ，

∴BE=AB﹣AE= ﹣ =2

【解析】（1）连结OD．先证明OD是△ABC的中位线，根据中位线的性质得到OD∥AB，再由DE⊥AB，得出OD⊥EF，根据切线的判定即可得出直线EF是⊙O的切线；（2）先由OD∥AB，得出∠COD=∠A，再解Rt△DOF，根据余弦函数的定义得到cos∠FOD= = ，设⊙O的半径为R，解方程 = ，求出R= ，那么AB=2OD= ，解Rt△AEF，根据余弦函数的定义得到cosA= =v，求出AE= ，然后由BE=AB﹣AE即可求解．
【考点精析】认真审题，首先需要了解切线的判定定理(切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线)．