题目内容
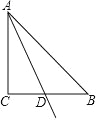
【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
【答案】解:(1)证明:∵CF平分∠DCE,∴∠1=∠2=![]() ∠DCE。
∠DCE。
∵∠DCE=90°,∴∠1=45°。
∵∠3=45°,∴∠1=∠3。∴AB∥CF。
(2)∵∠D=30°,∠1=45°,
∴∠DFC=180°﹣30°﹣45°=105°。
【解析】
试题(1)首先根据角平分线的性质可得∠1=45°,再有∠3=45°,再根据内错角相等两直线平行可判定出AB∥CF;
(2)利用三角形内角和定理进行计算即可.
试题解析:(1)∵CF平分∠DCE,∴∠1=∠2=![]() ∠DCE,∵∠DCE=90°,∴∠1=45°,∵∠3=45°,∴∠1=∠3,∴AB∥CF(内错角相等,两直线平行);
∠DCE,∵∠DCE=90°,∴∠1=45°,∵∠3=45°,∴∠1=∠3,∴AB∥CF(内错角相等,两直线平行);
(2)∵∠D=30°,∠1=45°,∴∠DFC=180°﹣30°﹣45°=105°.

练习册系列答案
相关题目