题目内容
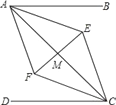
【题目】如图，已知：AB∥CD，∠BAE=∠DCF，AC，EF相交于点M，有FM=EM．
（1）求证：AE∥CF；
（2）若AM平分∠FAE，求证：FE垂直平分AC．
【答案】（1）证明见解析；（2）证明见解析．
【解析】
（1）先根据AB∥CD得出∠BAC=∠DCA，再由∠BAE=∠DCF可知∠EAM=∠FCM，故可得出结论；
（2）先由AM平分∠FAE得出∠FAM=∠EAM，再根据∠EAM=∠FCM可知∠FAM=∠FCM，故△FAC是等腰三角形，通过证明△AME≌△CMF，得到AM=CM，由等腰三角形三线合一的性质即可得出结论．
（1）∵AB∥CD，∴∠BAC=∠DCA．
又∵∠BAE=∠DCF，∴∠EAM=∠FCM，∴AE∥CF；
（2）∵AM平分∠FAE，∴∠FAM=∠EAM．
又∵∠EAM=∠FCM，∴∠FAM=∠FCM，∴AF=FC．
在△AME和△CMF中，∵∠AME=∠CMF，∠EAM=∠FCM，EM=FM，∴△AME≌△CMF，∴AM=CM，∴EF垂直平分AC．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某校举行了“文明在我身边”摄影比赛．已知每幅参赛作品成绩记为x分(60≤x＜100)．校方从600幅参赛作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题：
(1)统计表中c的值为________；样本成绩的中位数落在分数段________中；
(2)补全频数直方图；
(3)若80分以上(含80分)的作品将被组织展评，试估计全校被展评的作品数量是多少．
