Question

【题目】在△ABC中，已知AB=AC，∠BAC=90°，E为边AC上一点，连接BE．

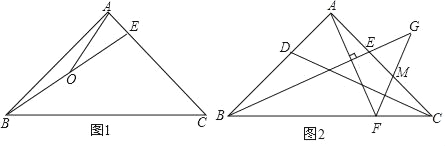
(1)如图1，若∠ABE=15°，O为BE中点，连接AO，且AO=1，求BC的长；

(2)如图2，D为AB上一点，且满足AE=AD，过点A作AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M，求证：BG=AF+FG．

Answer 1

【答案】（1） （2）证明见解析

【解析】

（1）如图1中，在AB上取一点M，使得BM=ME，连接ME．，设AE=x，则ME=BM=2x，AM=x，根据AB2+AE2=BE2，可得方程（2x+x）2+x2=22，解方程即可解决问题．
（2）如图2中，作CQ⊥AC，交AF的延长线于Q，首先证明EG=MG，再证明FM=FQ即可解决问题．

解：如图 1 中，在 AB 上取一点 M，使得 BM=ME，连接 ME．

在 Rt△ABE 中，∵OB=OE，

∴BE=2OA=2，

∵MB=ME，

∴∠MBE=∠MEB=15°，

∴∠AME=∠MBE+∠MEB=30°，设 AE=x，则 ME=BM=2x，AM=x，

∵AB2+AE2=BE2，

∴，

∴x= （负根已经舍弃），

∴AB=AC=（2+ ） ，

∴BC= AB= +1．

作 CQ⊥AC，交 AF 的延长线于 Q，

∵ AD=AE ，AB=AC ，∠BAE=∠CAD，

∴△ABE≌△ACD（SAS），

∴∠ABE=∠ACD，

∵∠BAC=90°，FG⊥CD，

∴∠AEB=∠CMF，

∴∠GEM=∠GME，

∴EG=MG，

∵∠ABE=∠CAQ，AB=AC，∠BAE=∠ACQ=90°，

∴△ABE≌△CAQ（ASA），

∴BE=AQ，∠AEB=∠Q，

∴∠CMF=∠Q，

∵∠MCF=∠QCF=45°，CF=CF，

∴△CMF≌△CQF（AAS），

∴FM=FQ，

∴BE=AQ=AF+FQ=AF=FM，

∵EG=MG，

∴BG=BE+EG=AF+FM+MG=AF+FG．