题目内容
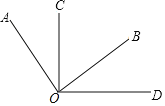
【题目】如图,∠AOB=∠COD=90
(1)若∠BOC=32,∠AOD的度数是多少?
(2)若∠AOD=132,∠BOC的度数是多少?
【答案】(1)∠AOD=148°(2)∠BOC=48°(3)∠AOC=∠BOD
【解析】试题分析:(1)根据∠COD=∠BOD+∠BOC,∠AOB=∠AOC+∠BOC,可以解出∠AOD的度数;(2)同(1);(3)在将(1)与(2)的答案算出来以后,总结即可.
试题解析:
(1)因为:∠COD=∠BOD+∠BOC,∠AOB=∠AOC+∠BOC,
又因为:∠AOB=∠COD=90°,
所以∠AOC=∠AOB-∠BOC=90°-32°=58°,∠AOD=∠COD+∠AOC=90°+58°=148°;
(2)因为:∠COD=∠BOD+∠BOC,∠AOB=∠AOC+∠BOC,
又因为:∠AOB=∠COD=90°,
所以∠AOC=∠AOB-∠BOC=90°-48°=42°,∠AOD=∠COD+∠AOC=90°+42°=132°, ∠BOC=48°
(3)由(1)和(2)可知,∠AOC=∠BOD,
改变∠BOC的大小此结论依然成立,
因为∠AOC=∠AOB-∠BOC,∠BOD=∠COD-∠BOC,
又因为∠AOC=∠BOD,所以∠AOC=∠BOD.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如下表:经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解析式:_____
x | 0 | 1 | 2 | 3 | 4 |
y | 3 | 0 | ﹣2 | 0 | 3 |
【题目】已知一次函数y=kx+b中,x取不同值时,y对应的值列表如下:
x | … | -m2-1 | 2 | 3 | … |
y | … | -1 | 0 | n2+1 | … |
则不等式kx+b>0(其中k,b,m,n为常数)的解集为( )
A.x>2
B.x>3
C.x<2
D.无法确定