题目内容
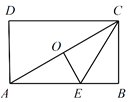
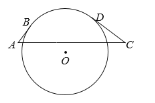
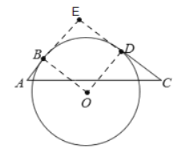
【题目】如图,AB、CD是⊙O的切线,B、D为切点,AB=2,CD=4,AC=10.若∠A+∠C=90°,则⊙O的半径是_______.
【答案】4
【解析】
连接OB,OD,延长AB,CD交于点E,先证四边形OBED为正方形,设半径为x,在Rt△ACE中根据勾股定理建立方程,解出x即可.
解:连接OB,OD,延长AB,CD交于点E,
∵AB、CD是⊙O的切线,B、D为切点,
∴∠EBO=∠EDO=90°,
∵∠A+∠C=90°,
∴∠AEC=90°,
∴四边形OBED为矩形,
∵OB=OD,
∴四边形OBED为正方形,
设半径为x,
∵AB=2,CD=4,AC=10,
∴AE=2+x,CE=4+x,
在Rt△ACE中,![]() ,
,
∴![]() ,
,
解得:![]() (舍去),
(舍去),
∴⊙O的半径为4,
故答案为:4.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目