Question

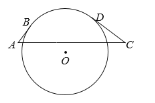
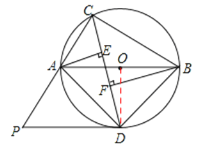
【题目】如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O于点D，过点D作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．

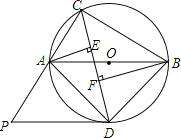
（1）求证：EF +AE= BF ；

（2）求证：△PDA∽△PCD ；

（3）若AC=6，BC=8，求线段PD的长．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】

（1）利用圆的性质，证明△ADE≌△DBF可得到结论，

（2）连接OD，证明∠PDA＝∠ACD＝∠ADO =45°，从而可得结论，

（3）利用圆的性质，得到△ACE，△DAB为等腰直角三角形，求解的长，利用△PDA∽△PCD，从而可得答案．

（1）证明：为直径，

∵∠ACB的平分线交⊙O于点D，

∴∠ACD=∠BCD=45°，

∴

∴AD=BD

∵AB是⊙O的直径，

∴∠ADB=∠ADE+∠BDF=90°，

∵AE⊥CD，BF⊥CD，

∴∠AED=∠BFD=90°，

∴∠FBD+∠BDF=90°，

∴∠FBD=∠ADE，

在△ADE和△DBF中

，

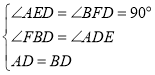∴△ADE≌△DBF（AAS）

∴BF=DE，AE=DF，

∵EF + DF = DE

∴EF + AE = BF

（2）证明：如图，连接OD

∵∠ACD=∠BCD=45°，

∴AD=BD

∴∠DAB＝∠ABD＝45°．

∴△DAB为等腰直角三角形．

∵AB是直径,O是圆心

∴∠ACD＝∠ADO＝∠BDO =45°.

∵PD为⊙O的切线，

∴OD⊥PD.

∴∠PDA＝∠ACD＝∠ADO =45°.

又∵∠DPA＝∠CPD，

∴△PDA∽△PCD，

（3）在Rt△ACB中，

∵△DAB为等腰直角三角形，

∴AD=DB=，

∵AE⊥CD，∠ACD＝45°

∴△ACE为等腰直角三角形．

∴AE=CE=

在Rt△AED中，

∵△PDA∽△PCD.

∴.

∴PA＝，PC＝.

又PC＝PA＋AC，

∴＋6＝，

解得：PD＝