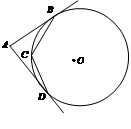Question

如图，点A、B、C在上，且∠COB＝53°，CD⊥OB，垂足为D，当时，求∠OBA的度数。

Answer 1

53°.

试题分析：过点O作OE⊥AB于点E，垂足为E，根据垂径定理可知BE=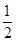AB，再由OD=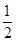AB可知BE=OD，在Rt△OBE与Rt△OCD中，根据HL定理可得出Rt△OBE≌Rt△OCD，再由全等三角形的对应角相等即可得出结论．
试题解析：过点O作OE⊥AB于点E，垂足为E，

∵O是圆心，点AB在⊙O上，OE⊥AB，
∴BE=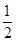AB，
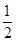∵OD=AB，
∴BE=OD，
∵点B、C在⊙O上，
∴OB=OC，
∵CD⊥OB，
∴∠ODC=90°，
∵OE⊥AB，
∴∠OEB=90°，
在Rt△OBE与Rt△OCD中，
，
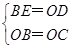∴Rt△OBE≌Rt△OCD，
∴∠OBA=∠COB，
∵∠COB=53°，
∴∠OBA=53°．
考点: 1.垂径定理；2.全等三角形的判定与性质．