题目内容
【题目】如图，已知AB为⊙O的直径，点C为半圆ACB上的动点（不与A、B两点重合），过点C作弦CD⊥AB，∠OCD的平分线交圆于点P，则点P的位置有何规律？请证明你的结论．
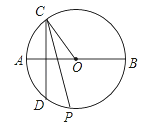
【答案】点P为半圆AB的中点．
【解析】
连接OP，如图，根据角平分线的定义得∠PCD=∠PCO，而∠PCO=∠OPC，则∠PCD=∠OPC，根据平行线的判定得OP∥CD，由于CD⊥AB，根据平行线的性质得到OP⊥AB，然后根据垂径定理即可得到弧PA=弧PB．
点P为半圆AB的中点．理由如下：
连接OP，如图，
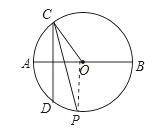
∵∠OCD的平分线交圆于点P，
∴∠PCD=∠PCO，
∵OC=OP，
∴∠PCO=∠OPC，
∴∠PCD=∠OPC，
∴OP∥CD，
∵CD⊥AB，
∴OP⊥AB，
∴弧PA=弧PB，
即点P为半圆的中点．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
