题目内容
【题目】如图，为一圆洞门．工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑，点A、B、C、D在⊙O上，CE⊥AB于E，DF⊥AB于F，且AB＝2
，EF＝
，
＝120°．
(1)求出圆洞门⊙O的半径；
(2)求立柱CE的长度．
【答案】(1)2;(2)
.
【解析】
（1）作
于
，连接
、
，根据垂径定理和圆心角定理可得
长度及
的角度，则在
中，根据的正弦值，可得半径的长度；（2）作
于
，连接
，易证四边形
是矩形，则
，
，在
中，根据勾股定理可得
长，则可得
的长度.
解：（1）作于，连接、，如图，
∵
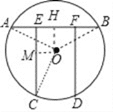
的度数为120°，
，
∴
，
∴
，
在中，
，
∴
，即圆洞门
的半径为2；
（2）作于，连接．
∵中，
，
∵，，
∴四边形是矩形，
∵
，
∴，，
在中，
，
∴
，
∴立柱的长度为．
练习册系列答案
相关题目
