Question

【题目】【提出问题】

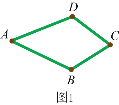
（1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．

【类比探究】

（2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．

【拓展延伸】

（3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

Answer 1

【答案】见解析

【解析】解：（1）证明：∵△ABC、△AMN是等边三角形，∴AB=AC，AM=AN，∠BAC=∠MAN=60°。

∴∠BAM=∠CAN。

∵在△BAM和△CAN中，，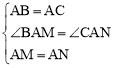

∴△BAM≌△CAN（SAS）。∴∠ABC=∠ACN。

（2）结论∠ABC=∠ACN仍成立。理由如下：

∵△ABC、△AMN是等边三角形，∴AB=AC，AM=AN，∠BAC=∠MAN=60°。

∴∠BAM=∠CAN。

∵在△BAM和△CAN中，，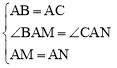

∴△BAM≌△CAN（SAS）。∴∠ABC=∠ACN。

（3）∠ABC=∠ACN。理由如下：

∵BA=BC，MA=MN，顶角∠ABC=∠AMN，∴底角∠BAC=∠MAN。

∴△ABC∽△AMN。∴。

又∵∠BAM=∠BAC﹣∠MAC，∠CAN=∠MAN﹣∠MAC，∴∠BAM=∠CAN.

∴△BAM∽△CAN。∴∠ABC=∠ACN。

（1）利用SAS可证明△BAM≌△CAN，继而得出结论。

（2）也可以通过证明△BAM≌△CAN，得出结论，和（1）的思路完全一样。

（3）首先得出∠BAC=∠MAN，从而判定△ABC∽△AMN，得到，根据∠BAM=∠BAC﹣

∠MAC，∠CAN=∠MAN﹣∠MAC，得到∠BAM=∠CAN，从而判定△BAM∽△CAN，得出结论。