Question

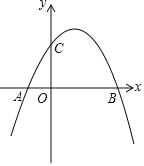
【题目】如图，抛物线y＝ax2+bx+4 经过点A（﹣3，0），点 B 在抛物线上，CB∥x轴，且AB 平分∠CAO．则此抛物线的解析式是___________．

Answer 1

【答案】y=-x2+x+4

【解析】

先计算出AC=5，再证明CB=CA=5，则B（5，4），然后利用待定系数法求抛物线解析式．

解：∵抛物线y=ax2+bx+4与y轴交于点C，

∴C（0，4），

∴OC=4，

∵A（-3，0），

∴OA=3，

∴AC=5，

∵AB平分∠CAO，

∴∠BAC=∠BAO，

∵BC∥x轴，

∴∠CBA=∠BAO，

∴∠BAC=∠CBA，

∴CB=CA=5，

∴B（5，4）．

把A（-3，0）、B（5，4）代入y=ax2+bx+4，

得，解得，

∴抛物线解析式为y=-x2+x+4．

故答案为y=-x2+x+4．