题目内容
【题目】已知![]() ,
,![]() ,D为直线BC上一点,E为直线AC上一点,
,D为直线BC上一点,E为直线AC上一点,![]() ,设
,设![]() ,
,![]() .
.
(1)如图1,若点D在线段C上,点E在线段AC上,![]() ,
,![]() ,则
,则![]() ______
______![]() ;
;![]() ________
________![]() .
.
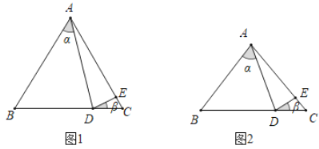
(2)如图2,若点D在线段BC上,点E在线段AC上,则![]() ,
,![]() 之间有什么关系式?它说明理由.
之间有什么关系式?它说明理由.
(3)是否存在不同于(2)中的![]() ,
,![]() 之间的关系式?请写出这个关系式(写出一种即可),说明理由:若不存在,请说明理由.
之间的关系式?请写出这个关系式(写出一种即可),说明理由:若不存在,请说明理由.
【答案】(1)20,10;(2)α=2β,理由见解析;(3)α=2β-180°或α=180°-2β,理由见解析
【解析】
(1)先利用等腰三角形的性质求出∠DAE,进而求出∠BAD,利用外角的性质求出∠ADC,进而可求出β的值;
(2)设∠ABC=x,∠AED=y,由三角形外角的性质可得y=β+x,α+x=y+β,整理可得![]() ,
,![]() 之间的关系;
之间的关系;
(3)①当点E在CA的延长线上,设∠ABC=x,∠ADE=y,由三角形外角的性质得x+α=β-y,由三角形内角和得x+y+β=180°,整理即可得出结论;
②当点E在CA的延长线上,点D在CB的延长线上,同①的方法即可得出结论.
解:(1)∵AB=AC,∠ABC=60°,
∴∠BAC=60°,
∵AD=AE,∠ADE=70°,
∴∠DAE=180°-2∠ADE=40°,
∴α=∠BAD=60°-40°=20°,
∴∠ADC=∠BAD+∠ABD=60°+20°=80°,
∴β=∠CDE=∠ADC-∠ADE=10°,
故答案为:20,10;
(2)α=2β,
设∠ABC=x,∠AED=y,
∴∠ACB=x,∠AED=y,
在△DEC中,y=β+x,
在△ABD中,α+x=y+β=β+x+β,
∴α=2β;
(3)①当点E在CA的延长线上,点D在线段BC上,
如图1
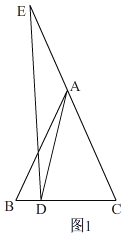
设∠ABC=x,∠ADE=y,
∴∠ACB=x,∠AED=y,
在△ABD中,x+α=β-y,
在△DEC中,x+y+β=180°,
∴α=2β-180°,
②当点E在CA的延长线上,点D在CB的延长线上,
如图2,
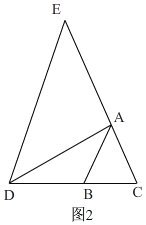
设∠ABC=x,∠ADE=y,
∴∠ACB=x,∠AED=y,
在△ABD中,x=α+β-y,
在△DEC中,x+y+β=180°,
∴α=180°-2β.
综上可知,不同于(2)的结论有:α=2β-180°或α=180°-2β.

 阅读快车系列答案
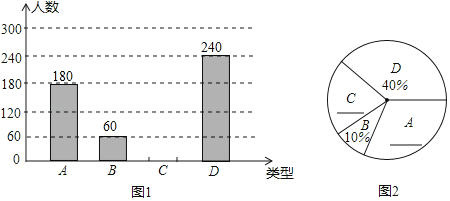
阅读快车系列答案【题目】某区教科院想了解该区中考数学试题中统计题的得分情况,从甲、乙两所学校各随机抽取了20名学生的学生成绩如下.(该题满分10分,学生得分均为整数)甲学校20名学生成绩(单位:分)分别为:7,7,8,9,8,6,7,8,8,10,7,9,6,8,7,8,9,7,8,9.乙学校20名学生学生成绩的条形统计图如图所示:
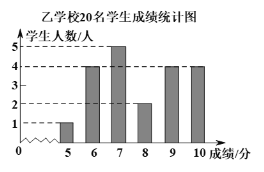
经过对两校这20名学生成绩的整理,得到分析数据如下表:
组别 | 极差 | 平均分 | 中位数 | 方差 |
甲 | 4 | b | 8 | 1.05 |
乙 | a | 7.8 | c | 2.46 |
(1)求出表中的a、b、c的值.
(2)该题得分8分及其以上即为优秀,已知甲学校有1200人,请估算甲学校的优秀人数有多少人?
(3)请你结合以上分析数据说明试题中统计题得分优秀的理由.