Question

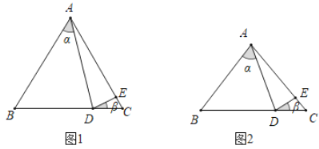
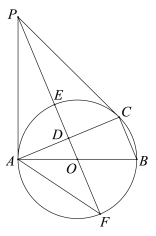
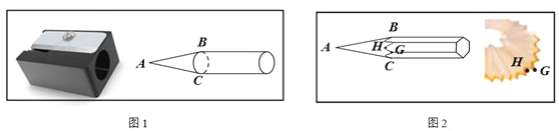
【题目】已知如图1，圆柱体铅笔插入卷笔刀充分卷削，得到底面直径BC为2的圆锥，∠BAC＝30°．底面边长为1的正六棱柱铅笔插入卷削，得到如图2所示铅笔和锯齿状木屑（木屑厚度忽略不计），木屑锯齿齿锋点G相邻凹陷最低点为H，则AG＝________，GH＝________．

Answer 1

【答案】

【解析】

抽象图形，利用等腰三角形的性质和三角形外角的性质，可证得∠GEO＝30°，再结合已知条件求出OG，EG的长，利用解直角三角形求出EO的长，从而可求出OA的长，然后利用勾股定理求出AG的长；底面边长为1的正六棱柱铅笔插入卷削，如图，可得到△OGK是等边三角形，利用解直角三角形求出OM，MN的长，再利用平行线分线段成比例定理可求出MH的长，然后证明△HMG是等腰直角三角形，继而可求出HG的长.

解：如图，

∵∠BAC＝30°，

∴∠GAO＝15°，

∵AE＝EG，

∴∠GAO＝∠AGE＝15°

∴∠GEO＝∠AGE＋∠GAO＝30°,

∵圆锥的底面直径为2,

∴OG＝1，

在Rt△AOG中，EG＝2OG＝2，

∴EO＝EGcos∠GEO＝2×cos30°＝,

∴OA＝AE＋OE＝2＋,

∴；

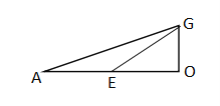
∵底面边长为1的正六棱柱铅笔插入卷削，如图，

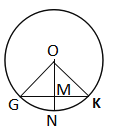
∴△OGK是边长为1的等边三角形，

∴OM＝OGsin60°＝，

∴MN＝1－，

如图，

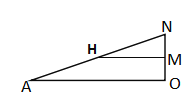
∵MH∥AO，

∴，

∴，

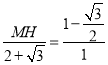解之：MH＝，

∵GK=1，HG=HK，HM⊥GK，

∴△HKG是等腰直角三角形，

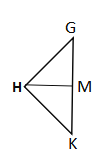
∴△HMG是等腰直角三角形，

∴即，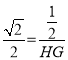

解之：HG＝.

故答案为：；.

此题考查正多边形和圆，勾股定理，等边三角形的判定及性质，等腰直角三角形的性质，平行线分线段成比例，解直角三角形，正确理解题中各部分之间的关系，根据题意画出对应的图形辅助解题是关键，体现数形结合是思想.