题目内容
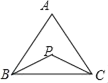
【题目】在△ABC中，∠A＝70°，若三角形内有一点P到三边的距离相等，则∠BPC＝_____；若三角形内有一点M到三个顶点的距离相等，则∠BMC＝_____．
【答案】125°； 140°
【解析】
根据三角形内到三边的距离相等的点是三内角平分线的交点、到三个顶点的距离相等的点是三边垂直平分线的交点及三角形内角和定理计算即可．
∵∠A＝70°，
∴∠ABC+∠ACB＝110°，
∵点P到三边的距离相等，
∴点P是三角形的内心，
∴∠PBC＝
∠ABC，∠PCB＝∠ACB，
∴∠PBC+∠PCB＝55°，
∴∠BPC＝125°，
∵点M到三个顶点的距离相等，
∴点M是三角形的外心，
∴∠BMC＝2∠A＝140°，
故答案为：125°；140°
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
