Question

【题目】如果正方形的边长为4，为边上一点，，为线段上一点，射线交正方形的一边于点，且，那么的长为__________．

Answer 1

【答案】或

【解析】

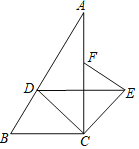
因为BM可以交AD，也可以交CD．分两种情况讨论：

①BM交AD于F，则△ABE≌△BAF．推出AF＝BE＝3，所以FD＝EC，连接FE，则四边形ABEF为矩形，所以M为该矩形的对角线交点，所以BM＝AC的一半，利用勾股定理得到AE等于5，即可求解；

②BM交CD于F，则BF垂直AE（通过角的相加而得）且△BME∽△ABE，则，所以求得BM等于．

分两种情况讨论：

①BM交AD于F，

∵∠ABE＝∠BAF＝90°，AB＝BA，AE＝BF，

∴△ABE≌△BAF（HL）

∴AF＝BE，

∵BE＝3，

∴AF＝3，

∴FD＝EC，

连接FE，则四边形ABEF为矩形，

∴BM＝AE，

∵AB＝4，BE＝3，

∴AE＝=5，

∴BM＝；

②BM交CD于F，

∵△ABE≌△BCF，

∴∠BAE＝∠CBF，

∵∠BAE＋∠BEA＝90°，

∴∠BEM＋∠EBM＝90°，

∴∠BME＝90°，

即BF垂直AE，

∴△BME∽△ABE，

∴，

∵AB＝4，AE＝5，BE＝3，

∴BM＝．

综上，故答案为：或