题目内容
如图，直线y=
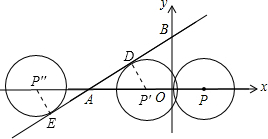
x+
与x轴、y分别相交与A、B两点，圆心P的坐标为（1，0），圆P与y轴相切与点O．若将圆P沿x轴向左移动，当圆P与该直线相交时，令圆心P的横坐标为m，则m的取值范围是______．
| ||
| 3 |
| 3 |
令y=0，则
x+
=0，
解得x=-3，
则A点坐标为（-3，0）；
令x=0，则y=
，
则B点坐标为（0，
），
则tan∠BAO=
，
则∠BAO=30°，
作⊙P′与⊙P″切AB于D、E，
连接P′D、P″E，则P′D⊥AB、P″E⊥AB，
则在Rt△ADP′中，AP′=2×DP′=2，
同理可得，AP″=2，
则P′横坐标为-3+2=-1，P″横坐标为-1-4=-5，
故P横坐标m的取值范围为：-5＜m＜-1，
故答案为：-5＜m＜-1
| ||
| 3 |
| 3 |
解得x=-3，
则A点坐标为（-3，0）；
令x=0，则y=
| 3 |
则B点坐标为（0，
| 3 |
则tan∠BAO=
| ||
| 3 |
则∠BAO=30°，
作⊙P′与⊙P″切AB于D、E，
连接P′D、P″E，则P′D⊥AB、P″E⊥AB，
则在Rt△ADP′中，AP′=2×DP′=2，
同理可得，AP″=2，
则P′横坐标为-3+2=-1，P″横坐标为-1-4=-5，
故P横坐标m的取值范围为：-5＜m＜-1，
故答案为：-5＜m＜-1
练习册系列答案
相关题目
OB，OC的长分别是方程x2-4x+3=0的两根（OB＜OC）．
