题目内容
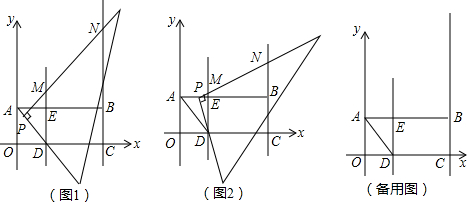
如图,在平面直角坐标系中,已知点A(-3,6),点B,点C分别在x轴的负半轴和正半轴上, OB,OC的长分别是方程x2-4x+3=0的两根(OB<OC).
OB,OC的长分别是方程x2-4x+3=0的两根(OB<OC).
(1)求点B,点C的坐标;
(2)若平面内有M(1,-2),D为线段OC上一点,且满足∠DMC=∠BAC,求直线MD的解析式;
(3)在坐标平面内是否存在点Q和点P(点P在直线AC上),使以O,P,C,Q为顶点的四边形是正方形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
 OB,OC的长分别是方程x2-4x+3=0的两根(OB<OC).
OB,OC的长分别是方程x2-4x+3=0的两根(OB<OC).(1)求点B,点C的坐标;
(2)若平面内有M(1,-2),D为线段OC上一点,且满足∠DMC=∠BAC,求直线MD的解析式;
(3)在坐标平面内是否存在点Q和点P(点P在直线AC上),使以O,P,C,Q为顶点的四边形是正方形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.
(1)x2-4x+3=0,
得x=3或1.
∵OB<OC,
∴B(-1,0),C(3,0).
(2)过A作AH⊥x轴于H点,则AH=CH=6,
∴∠ACB=45°,
同理(过M作MT⊥x轴于T点,则MT=CT=2 )可证:∠MCD=45°,
∴∠ACB=∠MCD.
又∵∠DMC=∠BAC,
∴△CAB∽△CMD,
∴
=
.
在△AHC中,AC=
=6
,同理MC=2
,
∴
=
,
∴DC=
,
∴OD=3-
=
,D(
,0).
设MD的解析式为y=kx+b(k≠0),则
,
∴
∴函数解析式是:y=3x-5.

(3)存在.Q1(3,3)或Q2(
,-
).
得x=3或1.
∵OB<OC,
∴B(-1,0),C(3,0).
(2)过A作AH⊥x轴于H点,则AH=CH=6,
∴∠ACB=45°,

同理(过M作MT⊥x轴于T点,则MT=CT=2 )可证:∠MCD=45°,
∴∠ACB=∠MCD.
又∵∠DMC=∠BAC,
∴△CAB∽△CMD,
∴
| AC |
| MC |
| BC |
| CD |
在△AHC中,AC=
| AH2+HC2 |
| 2 |
| 2 |
∴
| 4 |
| DC |
6
| ||
2
|
∴DC=
| 4 |
| 3 |
∴OD=3-
| 4 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
设MD的解析式为y=kx+b(k≠0),则
|
∴
|
∴函数解析式是:y=3x-5.

(3)存在.Q1(3,3)或Q2(
| 3 |
| 2 |
| 3 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
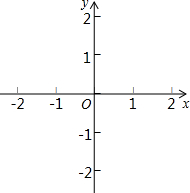
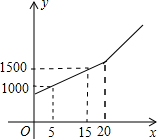
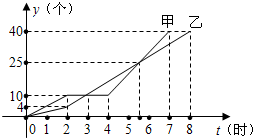 )与生产时间t(小时)的函数关系如图所示.
)与生产时间t(小时)的函数关系如图所示.