题目内容
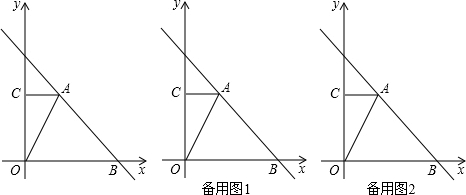
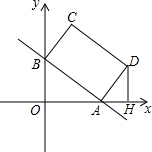
如图,已知A(-3,0),B(0,-4),P为直线y=-x+5在第一象限上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.则当x=______时,四边形ABCD面积的最大值为______.


设P的横坐标是x,则纵坐标是-x+5.则C的坐标是(x,0),D的坐标是(0,-x+5).
则AC=x+3,BD=-x+5+4=9-x,
则四边形ABCD面积S=
AC•BD=
(x+3)(9-x),
即S=-
x2+3x+
,
则当x=-
=3时,S有最大值是:-
×32+3×3+
=18.
故答案是:3,18.
则AC=x+3,BD=-x+5+4=9-x,
则四边形ABCD面积S=
| 1 |
| 2 |
| 1 |
| 2 |
即S=-
| 1 |
| 2 |
| 27 |
| 2 |
则当x=-
| 3 | ||
2×(-
|
| 1 |
| 2 |
| 27 |
| 2 |
故答案是:3,18.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
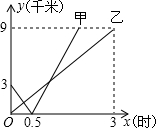
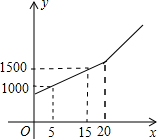
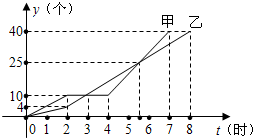 )与生产时间t(小时)的函数关系如图所示.
)与生产时间t(小时)的函数关系如图所示.