Question

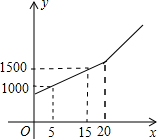
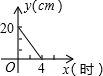
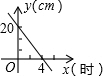
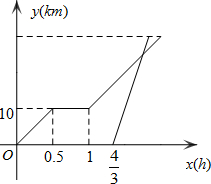
周末，小明骑自行车从家里出发到野外郊游．从家出发0.5小时后到达甲地，游玩一段时间后按原速前往乙地．小明离家1小时20分钟后，妈妈驾车沿相同路线前往乙地，如图是他们离家的路程y（km）与小明离家时间x（h）的函数图象．已知妈妈驾车的速度是小明骑车速度的3倍．
（1）求小明骑车的速度和在甲地游玩的时间；
（2）小明从家出发多少小时后被妈妈追上？此时离家多远？
（3）若妈妈比小明早10分钟到达乙地，求从家到乙地的路程．

Answer 1

（1）小明骑车速度：

10

0.5

=20(km/h)
在甲地游玩的时间是1-0.5=0.5（h）．

（2）妈妈驾车速度：20×3=60（km/h）
设直线BC解析式为y=20x+b₁，
把点B（1，10）代入得b₁=-10
∴y=20x-10
设直线DE解析式为y=60x+b₂，把点D（

4

3

，0）
代入得b₂=-80∴y=60x-80…
∴

y=20x-10 y=60x-80

解得

x=1.75 y=25

∴交点F（1.75，25）．
答：小明出发1.75小时（105分钟）被妈妈追上，此时离家25km．

（3）方法一：设从家到乙地的路程为m（km）
则点E（x₁，m），点C（x₂，m）分别代入y=60x-80，y=20x-10
得：x1=

m+80

60

，x2=

m+10

20

∵x2-x1=

10

60

=

1

6

∴

m+10

20

-

m+80

60

=

1

6

∴m=30．
方法二：设从妈妈追上小明的地点到乙地的路程为n（km），
由题意得：

n

20

-

n

60

=

10

60

∴n=5
∴从家到乙地的路程为5+25=30（km）．