题目内容
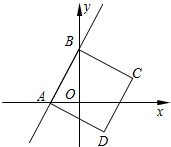
如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.

(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.

(1)∵一次函数y=x+1的图象与x轴交于点A,∴A(-1,0),
一次函数y=-2x+2的图象与x轴交于点B,∴B(1,0),
由
,解得
,∴P(
,
).
(2)设直线PA与y轴交于点Q,则Q(0,1),直线PB与y轴交于点M,则M(0,2),
∴四边形PQOB的面积=S△BOM-S△QPM=
×1×2-
×1×
=
.
一次函数y=-2x+2的图象与x轴交于点B,∴B(1,0),
由
|
|
| 1 |
| 3 |
| 4 |
| 3 |
(2)设直线PA与y轴交于点Q,则Q(0,1),直线PB与y轴交于点M,则M(0,2),
∴四边形PQOB的面积=S△BOM-S△QPM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |

练习册系列答案
相关题目

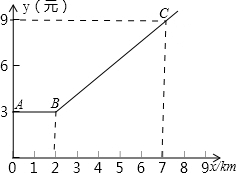



 )与生产时间t(小时)的函数关系如图所示.
)与生产时间t(小时)的函数关系如图所示.