Question

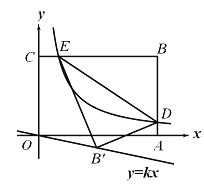
【题目】如图1，抛物线与轴交于点和点，与轴交于点，且满足，若对称轴在轴的右侧．

（1）求抛物线的解析式．

（2）如图，若点为线段上的一动点(不与重合)，分别以、为斜边，在直线的同侧作等腰直角三角形和，试确定面积最大时点的坐标．

（3）若，是抛物线上的两点，当，时，均有，求的取值范围．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）由二次函数与一元二次方程的关系，根据根与系数的关系得x+x=-2m，x·x=8m再联立，求解得m值，即可得出函数解析式；

（2）欲求△MNP的面积，确定△APM、△BNP是等腰直角三角形，即可求解；

（3）由（1）可知，函数的对称轴为：x=1，与关于对称轴对称，故其函数值相等，即可求解．

解：(1) 与轴交于和点,

是方程的两个根

，

即

解得，

对称轴轴在轴的右侧

（2）如图，和为等腰直角三角形

. .

为直角三角形

令，解得：，

，，

设，则

，

当，即时，最大，此时，所以

（3）由函数可知，对称轴为，则与关于对称轴对称，故其函数值相等，都为

又，时，均有，

结合函数图象可得：

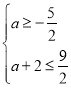解得：.